NumPy (Part II)#
What you will learn in this lesson:
Indexing and slicing NumPy arrays
Performing calculations on NumPy arrays
# Remember, we always have to import the package before starting to use it!
import numpy as np
Indexing and Slicing#
1D arrays in NumPy are indexed, sliced, and iterated over in the same way as lists and other Python data structures.
arr1d = np.arange(10)
arr1d
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
arr1d[5]
5
arr1d[5:8]
array([5, 6, 7])
Note that if we assign a scalar value to a slice of an array, all elements within that slice will be updated to the same value. This behavior is known as broadcasting.
arr1d[5:8] = 12
arr1d
array([ 0, 1, 2, 3, 4, 12, 12, 12, 8, 9])
Also, note that changes made to slices directly affect the original array, as slices are views, not copies.
arr_slice = arr1d[5:8]
arr_slice
array([12, 12, 12])
arr_slice[1] = 12345
arr1d
array([ 0, 1, 2, 3, 4, 12, 12345, 12, 8,
9])
You can set all elements to a given value by slicing the whole array:
arr_slice[:] = 64
arr_slice
array([64, 64, 64])
# See again how the original array also changed...
arr1d
array([ 0, 1, 2, 3, 4, 64, 64, 64, 8, 9])
Since NumPy is designed for handling large datasets, copying data unnecessarily could lead to performance and memory issues. To avoid this, NumPy uses views by default instead of copies.
Note
If you want a copy of a slice of an ndarray instead of a view, you will need to explicitly copy the array; for example arr[5:8].copy().
arr1d = np.arange(10)
arr_slice = arr1d[5:8].copy() # create a copy instead of a view
print(arr_slice)
arr_slice[:] = 64
# The slice has changed...
print(arr_slice)
# But the original array not
print(arr1d)
[5 6 7]
[64 64 64]
[0 1 2 3 4 5 6 7 8 9]
Higher Dimensional Arrays
In higher dimensional arrays, you index/slice arrays along each axis independently.
Here is an 2D example:
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr2d
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
arr2d[2]
array([7, 8, 9])
arr2d[0][2]
3
arr2d[0][1:3]
array([2, 3])
Slicing: Simplified notation
arr2d[0, 2]
3
arr2d[0, 1:3]
array([2, 3])
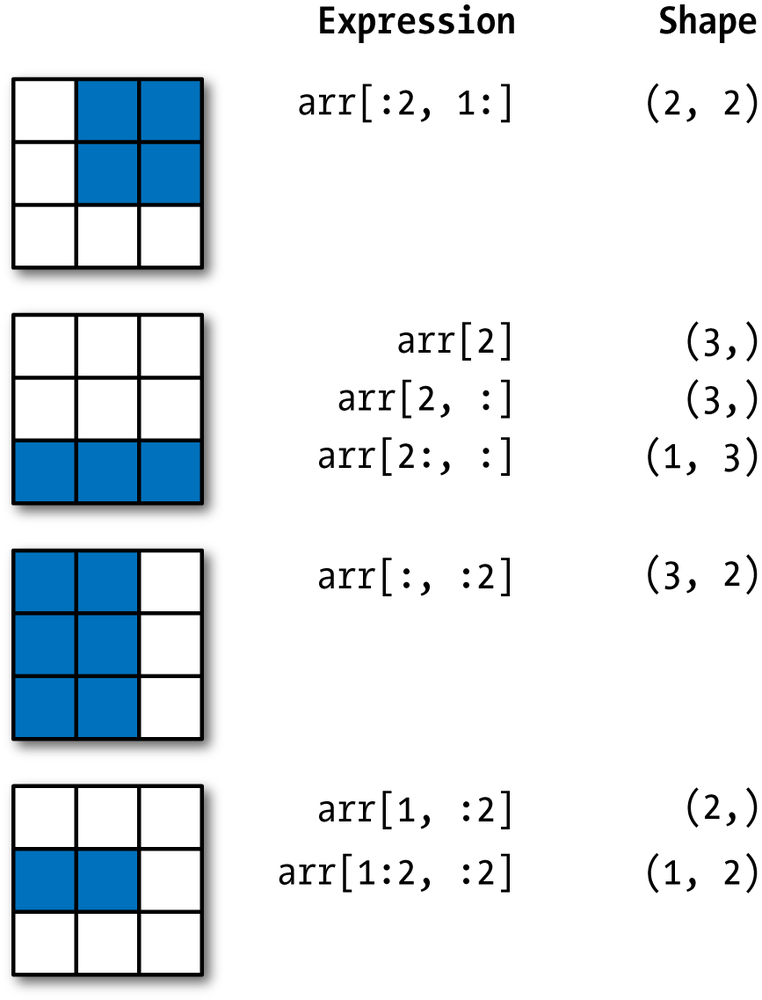
A nice visual of a 2D array
Two-Dimensional Array Slicing
The following is an example with 3D arrays:
arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print(arr3d)
print(arr3d.shape)
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
(2, 2, 3)
If you find NumPy’s way of showing the data a bit difficult to parse visually.
💡 Here is a way to visualize 3 and higher dimensional data:
[ # AXIS 0 CONTAINS 2 ELEMENTS (arrays)
[ # AXIS 1 CONTAINS 2 ELEMENTS (arrays)
[1, 2, 3], # AXIS 3 CONTAINS 3 ELEMENTS (integers)
[4, 5, 6] # AXIS 3
],
[ # AXIS 1
[7, 8, 9],
[10, 11, 12]
]
]
Each axis is a level in the nested hierarchy, i.e. a tree or DAG (directed-acyclic graph).
Each axis is a container.
There is only one top container.
Only the bottom containers have data.
In multidimensional arrays, if you omit indices for the later dimensions, the returned object will be a lower-dimensional ndarray that contains all the data from the higher-indexed dimensions.
So in the 2 × 2 × 3 array arr3d:
print(arr3d[0])
print(arr3d[0].shape)
[[1 2 3]
[4 5 6]]
(2, 3)
x = arr3d[1]
x
array([[ 7, 8, 9],
[10, 11, 12]])
print(x[0])
print(x[0].shape)
[7 8 9]
(3,)
Saving data before modifying an array.
old_values = arr3d[0].copy()
arr3d[0] = 42
arr3d
array([[[42, 42, 42],
[42, 42, 42]],
[[ 7, 8, 9],
[10, 11, 12]]])
Putting the data back.
arr3d[0] = old_values
arr3d
array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]])
Similarly, arr3d[1, 0] gives you all of the values whose indices start with (1, 0), forming a 1-dimensional array:
arr3d[1, 0]
array([7, 8, 9])
Boolean slicing#
In NumPy, we can mask arrays using boolean arrays. This is a crucial concept because it also applies to libraries like Pandas and R.
You can pass a boolean array to the array indexer (i.e., []), and it will return only the elements where the corresponding boolean value is True.
For example, let’s continue with the 2D array we used earlier:
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr2d
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# This will flag the elements that satisfy the condition of being greater than 5.
arr2d > 5
array([[False, False, False],
[False, False, True],
[ True, True, True]])
# We can use this to mask our array
arr2d[arr2d > 5]
array([6, 7, 8, 9])
Let’s look at a more detailed example, typical of a data science scenario. Assume we have two related arrays:
names, which represents the rows (observations) of a table.data, which holds the data associated with each feature.
In the example below, we will have 7 observations, and 4 features:
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
print(names)
data = np.random.standard_normal((7, 4))
print(data)
['Bob' 'Joe' 'Will' 'Bob' 'Will' 'Joe' 'Joe']
[[-0.7237047 -0.50762254 -0.48204371 -1.6133627 ]
[ 1.69705017 0.80812228 -0.66722951 1.33247531]
[-2.81200144 0.89421787 -0.02931852 -1.05156439]
[-1.06524316 -1.54260722 0.02495081 0.20867737]
[-0.14302032 0.81352009 -0.07620839 0.59158928]
[ 2.03311889 -0.3202367 -0.01237379 -1.41072045]
[-0.56663455 1.16679853 -1.34970156 -0.41449339]]
print(names.shape, data.shape)
(7,) (7, 4)
A comparison operation on an array returns an array of boolean values.
# This will return an array of booleans testing whether its value is equal to Bob
names == 'Bob'
array([ True, False, False, True, False, False, False])
# We can now use this as an array indexer to mask our data
data[names == 'Bob']
array([[-0.7237047 , -0.50762254, -0.48204371, -1.6133627 ],
[-1.06524316, -1.54260722, 0.02495081, 0.20867737]])
# We can also, at the same time, slice on the second axis to select data
data[names == 'Bob', 2:]
array([[-0.48204371, -1.6133627 ],
[ 0.02495081, 0.20867737]])
Here are some examples of boolean operations being applied:
# This selects all rows whose names are not 'Bob'
names != 'Bob'
data[~(names == 'Bob')]
array([[ 1.69705017, 0.80812228, -0.66722951, 1.33247531],
[-2.81200144, 0.89421787, -0.02931852, -1.05156439],
[-0.14302032, 0.81352009, -0.07620839, 0.59158928],
[ 2.03311889, -0.3202367 , -0.01237379, -1.41072045],
[-0.56663455, 1.16679853, -1.34970156, -0.41449339]])
cond = (names == 'Bob')
data[~cond]
array([[ 1.69705017, 0.80812228, -0.66722951, 1.33247531],
[-2.81200144, 0.89421787, -0.02931852, -1.05156439],
[-0.14302032, 0.81352009, -0.07620839, 0.59158928],
[ 2.03311889, -0.3202367 , -0.01237379, -1.41072045],
[-0.56663455, 1.16679853, -1.34970156, -0.41449339]])
# This selects all rows whose names are 'Bob' or 'Will'
mask = (names == 'Bob') | (names == 'Will')
print(mask)
print(data[mask])
[ True False True True True False False]
[[-0.7237047 -0.50762254 -0.48204371 -1.6133627 ]
[-2.81200144 0.89421787 -0.02931852 -1.05156439]
[-1.06524316 -1.54260722 0.02495081 0.20867737]
[-0.14302032 0.81352009 -0.07620839 0.59158928]]
# We can always update the masked parts of the original array using broadcasting
data[names != 'Joe'] = 7
data
array([[ 7. , 7. , 7. , 7. ],
[ 1.69705017, 0.80812228, -0.66722951, 1.33247531],
[ 7. , 7. , 7. , 7. ],
[ 7. , 7. , 7. , 7. ],
[ 7. , 7. , 7. , 7. ],
[ 2.03311889, -0.3202367 , -0.01237379, -1.41072045],
[-0.56663455, 1.16679853, -1.34970156, -0.41449339]])
~ instead of not to negate (flip) a value. Similarly, we use & and | instead of and and or.
Fancy Indexing#
In what is known as fancy indexing, we use arrays of index numbers to access specific data.
Instead of passing a single integer or a range using :, we pass a list of index numbers to the indexer.
# Let's create the following array
arr = np.empty((8, 4))
for i in range(8):
arr[i] = i
arr
array([[0., 0., 0., 0.],
[1., 1., 1., 1.],
[2., 2., 2., 2.],
[3., 3., 3., 3.],
[4., 4., 4., 4.],
[5., 5., 5., 5.],
[6., 6., 6., 6.],
[7., 7., 7., 7.]])
# This selects rows 4, 3, 0, and 6, in that order
arr[[4, 3, 0, 6]]
array([[4., 4., 4., 4.],
[3., 3., 3., 3.],
[0., 0., 0., 0.],
[6., 6., 6., 6.]])
# We can also index using negative index rules
arr[[-3, 0, -1]]
array([[5., 5., 5., 5.],
[0., 0., 0., 0.],
[7., 7., 7., 7.]])
Note that in this example, we are indexing along the first axis.
arr[[4, 3, 0, 6], :]
array([[4., 4., 4., 4.],
[3., 3., 3., 3.],
[0., 0., 0., 0.],
[6., 6., 6., 6.]])
We can also perform indexing along other axes:
# This selects the first and third column
arr[:, [0, 2]]
array([[0., 0.],
[1., 1.],
[2., 2.],
[3., 3.],
[4., 4.],
[5., 5.],
[6., 6.],
[7., 7.]])
What is happening in the previous examples is that we are combining fancy indexing with standard slicing.
# We could also do this
arr[:3, [0, 2]]
array([[0., 0.],
[1., 1.],
[2., 2.]])
We can also combine fancy indexing and simple indices:
arr[0, [0, 2]]
array([0., 0.])
And even with masking:
mask = np.array([1, 0, 1, 0, 0, 0, 1,0], dtype=bool)
arr[mask, :]
array([[0., 0., 0., 0.],
[2., 2., 2., 2.],
[6., 6., 6., 6.]])
Look at this example, now:
arr[[1, 5, 7, 2], [0, 3, 1, 2]]
array([1., 5., 7., 2.])
This is just creating an array with the elements (1,0), (5,3), (7,1), and (2,2).
If we want to index both axes to create a new array with specific rows and columns, we need to apply fancy indexing separately to each axis.
# We first index axis 0 (rows) and then axis 1 (columns)
arr[[1, 5, 7, 2], :][:,[0, 3, 1, 2]]
array([[1., 1., 1., 1.],
[5., 5., 5., 5.],
[7., 7., 7., 7.],
[2., 2., 2., 2.]])
# Here we first index axis 1 (columns) and then axis 0 (rows)
arr[:,[0, 3, 1, 2]][[1, 5, 7, 2], :]
array([[1., 1., 1., 1.],
[5., 5., 5., 5.],
[7., 7., 7., 7.],
[2., 2., 2., 2.]])
Inserting + Dropping Array Values#
Sometimes, it’s useful to exclude a specific index or drop the start or end of an array of values.
myarr = np.array([10,15,20,25,30,35,40,45,50])
np.insert: It inserts an element in a given index position.
# This insert the value 200 in the third position
np.insert(myarr, 2, 200)
array([ 10, 15, 200, 20, 25, 30, 35, 40, 45, 50])
np.delete: It drops an element in a specific index.
# This drops the third element
np.delete(myarr, 2)
array([10, 15, 25, 30, 35, 40, 45, 50])
In both cases, a new array is being created. That is, these functions do not modify the original array.
print(np.insert(myarr, 2, 200))
print(np.delete(myarr, 2))
print(myarr)
[ 10 15 200 20 25 30 35 40 45 50]
[10 15 25 30 35 40 45 50]
[10 15 20 25 30 35 40 45 50]
Basic calculations#
Addition and subtraction
a = np.array([1.0, 2.0, 3.0, 4.0])
b = np.array([2.0, 2.0, 2.0, 2.0])
print(a + b)
print(a + 2)
print(a - b)
print(a - 2)
[3. 4. 5. 6.]
[3. 4. 5. 6.]
[-1. 0. 1. 2.]
[-1. 0. 1. 2.]
Multiplication and division
print(a * b)
print(a * 2)
print(a / b)
print(a / 2)
[2. 4. 6. 8.]
[2. 4. 6. 8.]
[0.5 1. 1.5 2. ]
[0.5 1. 1.5 2. ]
More useful calculations#
NumPy includes over 500 built-in functions for performing operations, most of which can be applied directly to array data. Here are some common and straightforward examples:
# Start with the basic two-dimensional array we used above and manipulate in basic ways:
data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
arr2 = np.array(data2)
np.flip: It reverses the data of an array.
arr2_flipped = np.flip(arr2)
print(arr2_flipped)
[[8 7 6 5]
[4 3 2 1]]
np.copy: It copies an array to an entirely separate array.
arr2_copy = np.copy(arr2)
print(hex(id(arr2_copy)))
print(hex(id(arr2)))
0x7f73825a3450
0x7f735b82c030
np.concatenate: It combines all elements within an array into a single list.
arr2_concat = np.concatenate(arr2)
print(arr2_concat)
[1 2 3 4 5 6 7 8]
np.min: It calculates the min in an array.
arr2_min = np.min(arr2)
print(arr2_min)
1
np.max: It calculates the maximun element in an array.
arr2_max = np.max(arr2)
print(arr2_max)
8
np.mean: It calculates the mean.
# calculate the mean
arr2_mean = np.mean(arr2)
print(arr2_mean)
4.5
Let’s stop in this function for a bit. You can also calculate the mean along just one particular axis
help(np.mean)
Help on function mean in module numpy:
mean(a, axis=None, dtype=None, out=None, keepdims=<no value>, *, where=<no value>)
Compute the arithmetic mean along the specified axis.
Returns the average of the array elements. The average is taken over
the flattened array by default, otherwise over the specified axis.
`float64` intermediate and return values are used for integer inputs.
Parameters
----------
a : array_like
Array containing numbers whose mean is desired. If `a` is not an
array, a conversion is attempted.
axis : None or int or tuple of ints, optional
Axis or axes along which the means are computed. The default is to
compute the mean of the flattened array.
.. versionadded:: 1.7.0
If this is a tuple of ints, a mean is performed over multiple axes,
instead of a single axis or all the axes as before.
dtype : data-type, optional
Type to use in computing the mean. For integer inputs, the default
is `float64`; for floating point inputs, it is the same as the
input dtype.
out : ndarray, optional
Alternate output array in which to place the result. The default
is ``None``; if provided, it must have the same shape as the
expected output, but the type will be cast if necessary.
See :ref:`ufuncs-output-type` for more details.
keepdims : bool, optional
If this is set to True, the axes which are reduced are left
in the result as dimensions with size one. With this option,
the result will broadcast correctly against the input array.
If the default value is passed, then `keepdims` will not be
passed through to the `mean` method of sub-classes of
`ndarray`, however any non-default value will be. If the
sub-class' method does not implement `keepdims` any
exceptions will be raised.
where : array_like of bool, optional
Elements to include in the mean. See `~numpy.ufunc.reduce` for details.
.. versionadded:: 1.20.0
Returns
-------
m : ndarray, see dtype parameter above
If `out=None`, returns a new array containing the mean values,
otherwise a reference to the output array is returned.
See Also
--------
average : Weighted average
std, var, nanmean, nanstd, nanvar
Notes
-----
The arithmetic mean is the sum of the elements along the axis divided
by the number of elements.
Note that for floating-point input, the mean is computed using the
same precision the input has. Depending on the input data, this can
cause the results to be inaccurate, especially for `float32` (see
example below). Specifying a higher-precision accumulator using the
`dtype` keyword can alleviate this issue.
By default, `float16` results are computed using `float32` intermediates
for extra precision.
Examples
--------
>>> a = np.array([[1, 2], [3, 4]])
>>> np.mean(a)
2.5
>>> np.mean(a, axis=0)
array([2., 3.])
>>> np.mean(a, axis=1)
array([1.5, 3.5])
In single precision, `mean` can be inaccurate:
>>> a = np.zeros((2, 512*512), dtype=np.float32)
>>> a[0, :] = 1.0
>>> a[1, :] = 0.1
>>> np.mean(a)
0.54999924
Computing the mean in float64 is more accurate:
>>> np.mean(a, dtype=np.float64)
0.55000000074505806 # may vary
Specifying a where argument:
>>> a = np.array([[5, 9, 13], [14, 10, 12], [11, 15, 19]])
>>> np.mean(a)
12.0
>>> np.mean(a, where=[[True], [False], [False]])
9.0
arr2.shape
(2, 4)
# This is taking the mean along axis 0, i.e. along each row
np.mean(arr2, 0)
array([3., 4., 5., 6.])
# This is taking the mean along axis 1, i.e. along each column
np.mean(arr2, 1)
array([2.5, 6.5])
np.std: It calculates the standard deviation.
arr2_std = np.std(arr2)
print(arr2_std)
2.29128784747792
NumPy also provides many universal functions, or
ufuncs, which perform elementwise operations on data in ndarrays. You can think of them as fast, vectorized wrappers for simple functions that take one or more scalar values and return one or more scalar results. Many ufuncs perform simple elementwise transformations. For example:
# This takes the sin
print(np.sin(arr2))
# This takes the cos
print(np.cos(arr2))
# This computes the sqrt
print(np.sqrt(arr2))
# This computes the exponent
print(np.exp(arr2))
[[ 0.84147098 0.90929743 0.14112001 -0.7568025 ]
[-0.95892427 -0.2794155 0.6569866 0.98935825]]
[[ 0.54030231 -0.41614684 -0.9899925 -0.65364362]
[ 0.28366219 0.96017029 0.75390225 -0.14550003]]
[[1. 1.41421356 1.73205081 2. ]
[2.23606798 2.44948974 2.64575131 2.82842712]]
[[2.71828183e+00 7.38905610e+00 2.00855369e+01 5.45981500e+01]
[1.48413159e+02 4.03428793e+02 1.09663316e+03 2.98095799e+03]]
Note what happens if you apply np.sqrt to negative values:
np.sqrt(np.array([4, -3, 16, 9, -5]))
/tmp/ipykernel_38273/1198364157.py:1: RuntimeWarning: invalid value encountered in sqrt
np.sqrt(np.array([4, -3, 16, 9, -5]))
array([ 2., nan, 4., 3., nan])
nan is a special value in NumPy.
Practice exercises#
Exercise 33
Given the array below:
1- Extract the subarray containing the first two rows and the last three columns.
2- Reverse the third row.
3- Extract every second element from the entire array (flatten it into a 1D array).
arr_exec1 = np.array([[10, 20, 30, 40, 50],
[60, 70, 80, 90, 100],
[110, 120, 130, 140, 150],
[160, 170, 180, 190, 200]])
# Your answers from here
Exercise 34
Given the array below:
1- Select the elements at positions (0,1), (2,3), and (3,0) using fancy indexing.
2- Extract the second and fourth rows using fancy indexing.
3- Extract the first, third, and fourth elements from the first column using fancy indexing.
arr_exec2 = np.array([[5, 10, 15, 20],
[25, 30, 35, 40],
[45, 50, 55, 60],
[65, 70, 75, 80]])
# Your answers from here
Exercise 35
Considering the variable scores below as an array of student test scores, and classes the class each student belongs to, do the following:
1- Compute the mean score for each student (row-wise).
2- Compute the mean score for each test (column-wise).
3- Compute the overall standard deviation of all scores.
4- Subtract the mean of each test (column-wise) from the scores.
5- Use Boolean indexing to extract the scores of students from “Class A” and compute the mean score for “Class A”.
6- Use Boolean indexing to find the students in “Class B” who scored above 85 in their first test.
scores = np.array([[75, 80, 85, 90, 95],
[88, 92, 78, 85, 91],
[60, 75, 70, 65, 80],
[90, 85, 88, 92, 94],
[55, 60, 65, 70, 75],
[95, 100, 90, 85, 92],
[85, 89, 90, 87, 86],
[78, 80, 85, 82, 81],
[65, 70, 68, 72, 74],
[92, 94, 90, 88, 95]])
classes = np.array(['Class A', 'Class B', 'Class A', 'Class C',
'Class A', 'Class C', 'Class B', 'Class B',
'Class A', 'Class C'])
# Your answers from here
